
Max Planck Fellow Group: Inverse Problems
Inverse problems consist in reconstructing causes from observed effects. Such problems occur frequently in astrophysics as quantities of interest cannot be observed directly. Inverse problems are typically ill-posed in the sense that causes do not depend continuously on their effects and hence noise in the measurement of effects may be arbitrarily amplified by naïve reconstruction methods. For more information on inverse problems in general, see inverse problems group at the University of Göttingen.
A particular focus of this group are inversions for quantities in the interior of the Sun from correlation data of acoustic waves on the solar surface. This is a collaboration with the group of Laurent Gizon. One of our aims is to prove uniqueness results for these problems, i.e. that noiseless data, which in this case correspond to the imaginary part of Green’s function, uniquely determine the quantities of interest such as flow, sound speed, density, and absorption. Moreover, we develop accurate, stable and efficient reconstruction methods for these inverse problems. To some extent we are also involved in the development of efficient numerical solution methods of the time-harmonic wave equations describing the forward problems.
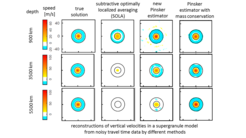
A further aim consists in the reconstruction of quantities in the photosphere from spectropolarimetric measurements in cooperation with the group of Sami Solanki.







